önceki

yazdır

Arş.Gör.Dr. Sabri AZGÜN

DİNAMİK STOKASTİK GENEL DENGE MODELLERİNİN TEST EDİLMESİ: EKONOMETRİK TAHMİN VE KALİBRASYON TESTING DYNAMIC STOCHASTIC GENERAL EQUILIBRIUM MODELS: CALIBRATION AND ESTIMATION

Özet

Dinamik stokastik genel denge modellerinin ampirik geçerliliğinin test edilmesi için iki temel yöntem söz konusudur: ‘kalibrasyon’ ve ‘tahmin’. Her iki yöntemin amacı da modellerin ampirik geçerliliğinin sınanmasıdır. Bununla birlikte iki yöntem de, metodolojik olarak farklı yaklaşımları yansıtmaktadır. Bu nedenle, doğal olarak her iki yöntemin de hem savunucuları hem de eleştirenleri vardır. Bu çalışmada dinamik stokastik genel denge metodolojisi açısından kalibrasyon ve tahmin yöntemlerinin avantajları ve dezavantajları ele alınmıştır.

Anahtar sözcükler: kalibrasyon, tahmin, dinamik stokastik genel denge modelleri, ekonomik metodoloji.

Abstract

There are two methods for testing the empirical validity of dynamic stochastic general equilibrium models: ‘calibration’ and ‘estimation’. The aim of the both methods is to test the empirical validity of the models. On the other hand, both methods reflect different methodological approaches. Naturally both have advocates and critics. In this study, the advantages and disadvantages of calibration and estimation with respect to dynamic stochastic general equilibrium methodology are considered.

Keywords: calibration, estimation, dynamic stochastic general equilibrium models, economic methodology.

1. Giriş

Ekonomideki bireylerin tercihlerinden hareket eden ve ekonominin genelini ele alan dinamik stokastik genel denge (DSGD) modelleri, makroiktisatta yaygın kullanılan analiz araçları haline gelmişlerdir. DSGD modelleri özlerinde teorik oldukları için, politika analizlerinde kullanılmadan önce ampirik geçerliliklerinin test edilmesi gerekmektedir. Bu ise modellerin gerçek ekonomilerde gözlemlenmiş makroekonomik verilerle karşılaştırılmaları demektir. Teorik modelin gerçek verilerle ne kadar örtüştüğünün test edilmesi için iki temel yaklaşım söz konusudur: ‘tahmin’ ve ‘kalibrasyon’.

Keynesyen modellerin aksine, DSGD modelleri mikroekonomik temellerden hareket ederler. Bu nedenle Keynesyen modellerden daha kompleks bir yapıya sahiplerdir. Modelleri kompleks hale getiren bir diğer özellik ise stokastik unsurlar içermeleridir. DSGD modellerinin amaçları bir anlamda gerçek ekonomilerdeki veri üretim süreçlerini (data generating process) modellemektir. Bu nedenle modellerde stokastik süreçlere ilişkin birtakım varsayımların yapılması gerekmektedir. DSGD modellerinin kompleks yapıları ima ettikleri ilişkilerin tümüyle analitik metotlar kullanılarak anlaşılmasını engellemektedir. Dolayısıyla modeli analitik olarak çözmek yerine, modelin öngörülerini anlayabilmek ve bu öngörüleri ekonomik veri ile karşılaştırmak için iki yol vardır. Bunlardan biri, uygun yapısal parametreler kullanılarak modelin bilgisayarlar yardımı ile nümerik olarak çözülmesi ve simülasyon yolu ile elde edilen yapay zaman serilerinin bir takım istatistiksel özelliklerinin ekonomik veri ile karşılaştırılmasıdır. Kabaca özetlenen bu yöntem kalibrasyon olarak adlandırılmaktadır. ‘Kalibrasyon’ kelimesi mühendislik kökenli bir kelime olup makine veya ölçme araçlarının ‘ince ayar’ yapılma işlemidir. İktisat metodolojisi bağlamında ise belli bir istatistiksel model varsayılmadan model parametrelerinin gerçek veriye göre ayarlanması işlemi olarak tanımlanabilir. Teorik modelin veri ile karşılaştırılması için izlenebilecek bir diğer yol ise, modelin yapısal parametrelerinin belli istatistiksel varsayımlar çerçevesinde ekonometrik yöntemlerle tahmin ve test edilmesidir. Bu yöntem ise kısaca ‘tahmin’ olarak adlandırılmaktadır.

Her iki yaklaşımın amacı da modelin geçerliliğinin sınanmasıdır. Bununla birlikte iki yaklaşım da, bu hedefe birbirlerinden tamamıyla farklı yönlerden yaklaşmaktadırlar. Kalibrasyon yaklaşımı teorik modelin yanlış olduğunu peşinen kabul etmektedir. Buradaki yanlış ifadesi modelin gerçek ekonomiyi birebir yansıtmadığı, sadece belli birtakım karakteristik özelliklerini açıklama potansiyeline sahip olması anlamında kullanılmaktadır. Buradan hareketle kalibrasyon işlemi modelin yapısal parametrelerinin gerçek veriye minimum kriterlerde benzeyen yapay veri üretebilecek şekilde belirlenmesi, yani kalibre edilmesidir.  Tahmin yaklaşımı ise modelin doğru veri üretim sürecini temsil ettiğini kabul eden boş hipotezin ekonometrik tekniklerle tahmin edilmesini öngörür.

Her iki yaklaşımın da destekçileri ve eleştirenleri vardır. Bu çalışmada kalibrasyon ve tahmin yaklaşımları DSGD modelleri çerçevesinde ele alınmıştır. Bu amaçla öncelikle DSGD metodolojisi ele alınmıştır. Daha sonra ise kalibrasyon ve tahmin yaklaşımları açıklanarak, her iki yaklaşımın da avantajları ve dezavantajları değerlendirilmiştir.

2. DSGD Metodolojisi

Sargent (1987:7), makro ekonomik araştırmaların amaçlarını “... gözlemlenen toplulaştırılmış ekonomik değişkenleri, ekonomik birimlerin motivasyonları ve kısıtları açısından yorumlamak ve hipotetik alternatif ekonomik politikaların sonuçlarını öngörmek” olarak tanımlamaktadır. Bu perspektiften bakıldığında, DSGD modelleri alternatif ekonomik politikaların analiz edilmesi için oldukça elverişli araçlardır. Bir kez uygun model oluşturulduktan sonra, modeldeki politika kurallarını veya karar kurallarını değiştirerek, alternatif politikaların etkileri analiz edilebilmektedir. DSGD modelleri, yapısal olma özellikleri nedeni ile, Lucas'ın (1976) deyimi ile “derin” parametreler değişmediği için Neoklasik Eleştiri'den etkilenmeden bu tür analizlere olanak sağlamaktadır.

Aynı doğrultuda, Lucas (1980) teorik iktisadın fonksiyonlarından birinin de, ekonomik politikaların test edilebileceği bir laboratuar görevi görecek, bütünüyle ve ayrıntılarıyla tanımlanmış yapay ekonomiler oluşturmak olduğunu söylemektedir. Buradan hareketle Lucas'a göre iktisatçıların görevi,

“... ‘girdi’ olarak spesifik ekonomik politika kurallarını kabul edecek ve ‘çıktı’ olarak da, bu ekonomik politikaların uygulanması durumunda ortaya çıkacak ilgili zaman serilerinin çalışma özelliklerini açıklayabilecek istatistikleri üretecek bir FORTRAN kodu [veya herhangi bir bilgisayar programı] yazmaktır”  (Lucas, 1980:709).

Bu sözlerle Lucas, iktisatçıların görevini tarif ederken aslında DSGD metodolojisini özetlemektedir. Kydland ve Prescott (1996) Lucas'ın yukarıda özetlediği bu süreci daha ayrıntılı bir şekilde sistematize etmişlerdir. Bu yazarların hesaplama deneyi (computational experiment) olarak tanımladıkları sürecin ilk adımı araştırma sorusunun ortaya konmasıdır. Daha sonra, ortaya konan soruya cevap verebileceği umulan bir model ekonomi oluşturulur. Oluşturulan bu model ekonomi, gerçek ekonomide gözlemlenen verilerden, mikro ekonometrik tekniklerle tahmin edilmiş yapısal parametreler kullanılarak ‘kalibre’ edilir. Bir sonraki adımda ise, kalibre edilmiş model kullanılarak nümerik simülasyonlar ile ilgilenilen zaman serileri üretilir ve gerçek ekonomide gözlemlenen zaman serileri ile karşılaştırılır. Yani model bir anlamda test edilir. Sürecin son aşaması ise, hipotetik alternatif politikaların sonuçlarının analiz edilmesidir.

Genellikle bir DSGD modelinin çatısı aşağıdaki dört temel kısımdan oluşmaktadır:

§   Model ekonominin yapısı/ekonomik çevre: Bu kısımda ekonomide ne tip malların mevcut olduğu, ekonomik bireylerin sayısı ve özellikleri, bu bireylerin tercih yapıları (amaç fonksiyonları), başlangıçtaki sermaye stokları veya emekleri, ekonomideki firma sayısı ve tipleri, kamu sektörü ve işlevi, üretim teknolojisi, piyasalar ve yapıları, ticaretin yapılış şekli, olayların zamanlaması, zaman periyotları ve rassal şokların kaynakları hakkında detaylı bilgiler yer alır. Diğer bir deyişle, bu kısım ekonominin yapısına ilişkin araştırmacının yapmış olduğu bütün varsayımları içerir.

§   Ekonomik aktörlerin optimal kararları: Bu kısımda ekonomik aktörlerin (bireyler, firmalar, devlet vs.), tüketicilerin bütçe kısıtları altında faydalarını maksimum yapmaları, ya da firmaların kar maksimizasyonunu hedeflemeleri gibi optimal davranışları tanımlanır. Ayrıca bu kısımda, karar değişkenleri ve durum (state) değişkenlerinin açıkça belirlenmesi gerekir. Örneğin, bireylerin optimizasyon sürecinde belirledikleri tüketim miktarı karar değişkeni iken, bu kararı verirken veri olarak aldıkları piyasa fiyatları ve mevcut sermaye stoğu durum değişkenleridir.

§   Şoklar: Bu kısımda, ekonomiyi etkileyen rassal şokların yapısı ve ortaya çıkış zamanlaması detaylı olarak verilir.

§   Denge şartları: Bu kısımda dengenin unsurları detaylı bir şekilde tanımlanır. Model ekonominin özelliklerine bağlı olmakla birlikte, genellikle bir DSGD modelinde denge, ekonomik birimlerin veri piyasa yapısı ve kaynak kısıtları altında, aldıkları optimizasyon kararları doğrultusunda oluşan fiyat ve tahsisat serilerinden oluşur.

Matematiksel olarak DSGD modelleri kesikli (discrete) veya sürekli (continuous) zaman çerçevesi kullanılarak oluşturulabilirler. Kesikli zaman kullanıldığında, zaman değişkeni  şeklinde tamsayılar ile ifade edilir. Sürekli zaman değişkeni ise belli bir zaman aralığında mümkün olan her değeri alabilir. Analitik olarak çözülebilen küçük bir sınıf model için, sürekli zaman ile çalışmak daha elverişlidir. Nümerik çözümler için ise bütün değişkenlerin kesikli olması gerekmektedir. Çünkü bilgisayarlar sürekli değişkenlerle işlem yapamazlar. Bu nedenle, DSGD modellerinin nümerik olarak çözülebilmeleri için ya kesikli değişkenler kullanılması, ya da zaman değişkeni de dahil olmak üzere, bütün sürekli değişkenlerin kesikli hale getirilmeleri gerekir.

Model ekonominin yapısına göre DSGD modelleri, Temsili Birey (representative agent) Modelleri, Heterojen Bireyler (heterogeneous agents) Modelleri ve Çakışan Kuşaklar (overlapping generations) Modelleri olarak üç temel kategoriye ayrılabilir. Bu üç farklı modelleme tekniğinin her birinin kendine özgü avantajları ve dezavantajları söz konusudur. Örneğin, temsili birey modelleri ile demografik analizler yapmak mümkün değildir. Bu tip analizler için çakışan kuşaklar modellerinin kullanılması gerekir. Benzer şekilde, eğer gelir dağılımı analiz edilmek isteniyorsa çakışan kuşaklar modellerinin tercih edilmesi uygun olacaktır.

2.1. Temsili Birey Modelleri

Literatürde en fazla eleştiri alan modeller olmasına rağmen, en yaygın kullanılan DSGD model tipi temsili birey (TB) modelleridir.[i] TB modellerinin makro iktisatçılar tarafından kullanımına ilişkin detaylı metodolojik tartışmalar için bkz. Hartley (2002). TB modellerinde, ekonomideki bütün bireyler (veya ‘hanehalkları’) birbirinin aynıdır. Diğer bir ifade ile, ekonomideki bütün bireyler aynı tercihlere ve aynı karar verme kurallarına sahiptir. Dolayısı ile, ekonomideki bütün bireylerin ‘temsili birey’ adı verilen tek bir birey veya hanehalkı ile temsil edilebilmesi mümkündür. Genellikle sonsuza dek yaşadıkları varsayılan bu temsili birey veya bireyler, ekonominin yapısına bağlı olarak yaşam boyu faydasını maksimum yapmayı amaçlarlar.

TB modellerinin en basit şekli Ramsey (1928) Modeli'dir.[ii] Ramsey, bu çalışmasında ‘Bir ülke, gelirinin ne kadarını tasarruf etmelidir?’ sorusunu yanıtlamak amacıyla dinamik bir model geliştirmiştir. Ramsey'in modelinde temsili ekonomik birey, hiçbir belirsizliğin olmadığı bir ekonomide her dönem tüketim ve yatırım miktarını belirlemek zorundadır. Temsili birey, bu kararı hayat boyu faydasını maksimum edecek şekilde oluşturmak zorundadır. Orijinal makalede bu birey hayali bir merkezi planlayıcıdır, fakat modellenecek ekonominin yapısına göre farklı şekillerde yorumlanabilir. Örneğin temsili birey, ürettiği tarım ürününün ne kadarını tüketip, ne kadarını ise gelecek yıl için saklaması gerektiğine karar vermek durumunda olan bir çiftçi olarak düşünülebilir.

I.2. Heterojen Bireyler Modelleri

Heterojen bireyler (HB) modellerinde ekonomide birbirlerinden farklı birden fazla birey vardır. Dolayısı ile ekonomideki bütün bireyler tek bir birey tarafından temsil edilemezler. Bireyler yetenekleri, eğitim durumları, zaman tercihleri, riske karşı tutumları ve istihdam durumları gibi birçok bakımdan farklılık gösterebilirler.

HB modelleri yardımıyla, gerçek makro ekonomik verilerde gözlemlenen ve TB modellerinin açıklayamadığı özellikler modellenebilmektedir (Rios-Rull, 1995). Örneğin, bir ekonomideki gelir ve servet dağılımını hangi faktörlerin ne ölçüde belirlediği HB modelleri yardımı ile analiz edilebilmektedir (örneğin bkz. Castadena vd. (1998) ve Li vd. (2000)).

HB modellerinin kullanıldığı bir  diğer önemli alan ise eksik (finansal) piyasalar konusudur. Eksik piyasalar, bir ekonomideki bireylerin kişisel bazı risklerle (idiosyncratic risks) karşı karşıya oldukları ve bu riskleri sigortalamak için gerekli mekanizmaların olmadığı durumlarda söz konusudur. Örneğin, ekonomideki bazı bireyler iş bulabilirken, bazıları işsiz kalabilir. Bunun gibi, bireylere özel risklerin sigortalanamadığı bir ekonomiyi modellemek için HB modelleri kullanılır. Böyle bir model yardımıyla işsizlik sigortası veya sosyal sigortalar gibi birçok değişik kamu politikası analiz edilebilir. Bütün risklerin sigortalanabildiği Arrow-Debreu piyasalarından ayrılan bu tip modeller, ‘eksik piyasalar’ adı altında geniş bir literatür oluşturmaktadır (Ljungqvist ve Sargent, 2000:ch17).

I.3. Çakışan Kuşaklar Modelleri

Samuelson tarafından (1958) yılında yapılan çalışmayı temel alan çakışan kuşaklar (ÇK) modellerinde, herhangi bir dönemde aynı anda hayatta olan birden fazla kuşak söz konusudur.[iii] ÇK ekonomisi, farklı zamanlarda doğan ve sınırlı yaşam sürelerine sahip bireylerden oluşur. Her birey  dönem yaşar ve ölür. Bireyler sınırlı bir yaşam süresine sahip olsa da, ekonomi sonsuza kadar varlığına devam eder. Herhangi bir t döneminde ekonomideki bireyler hayatlarının farklı dönemlerinde olacakları için, bu bireylerin tercih yapıları aynı olsa dahi farklı kararlar verebilirler. Bu özelliği nedeniyle ÇK modellerinde doğal bir heterojenlik ortaya çıkmaktadır. Ayrıca, bireylerin sınırlı bir yaşam süresine sahip olmaları, bu modeller yardımı ile hayat döngüsü (life-cycle) ekonomilerinin modellenebilmesini olanaklı hale getirmektedir.

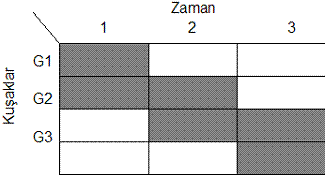
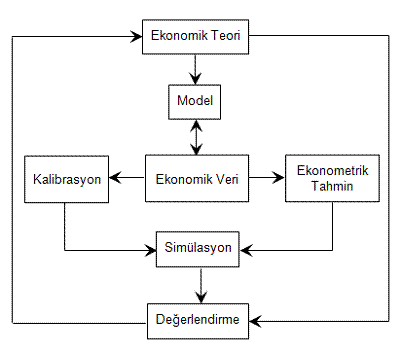
Şekil 1: Çakışan Kuşaklar Modelinin Demografik Yapısı

ÇK modellerinin en basit şekli iki dönemden oluşmaktadır. Bu modellerde, doğan her birey sadece iki dönem yaşamaktadır. Dolayısı ile, herhangi bir t döneminde ekonomide iki farklı kuşak vardır: yaşlılar ve gençler. Şekil 2'de iki dönemli ÇK ekonomisinin demografik yapısı görülmektedir.

Ekonomide birden fazla ve hayatlarının farklı dönemlerini yaşayan bireyler olması nedeniyle, ÇK modelleri ekonomide itibari (fiat) paranın varlığına olanak sağlamaktadır. ÇK ekonomilerinde para, kuşaklar arası kaynak aktarım aracı olarak talep görür. Ekonomideki bireyler bu işlevi nedeniyle, reel olarak herhangi bir getirisi olmasa dahi paraya bir değer atfederler. Bu nedenle ekonomi dengedeyken bireylerin ellerinde tuttukları paranın toplam değeri pozitiftir.[iv]

ÇK modellerinde, ekonomideki bireylerin N dönem sonra ölmeleri şart değildir. Yaari (1965) ve Blanchard (1985), bir ÇK ekonomisine yaşam belirsizliğini ekleyerek daha zengin bir model oluşturmuşlardır. Bu modellerde her birey N dönem sonra belli bir ölüm olasılığı ile karşı karşıyadır.

3. Teorik Model Ve Ekonomik Veri

Model ekonominin yapısı ile ilgili varsayım ne olursa olsun teorik modelin ekonomik veri ile ne kadar örtüştüğünün belirlenmesi önem taşımaktadır. Teorik modelin ampirik geçerliliğinin sınanması teorinin makroekonomik analizlerde kullanılmadan önce gerçekleştirilmesi geren bir aşamadır.  Makro ekonomik literatürde DSGD modellerinin ekonomik verilerle sınanması amacıyla iki farklı metot kullanılmaktadır: ‘tahmin’ ve ‘kalibrasyon’. Tahmin yönteminde, önce modelin gerçek ekonominin doğru bir tanımı olduğu varsayımı altında, modelin yapısal parametreleri En Çok Olabilirlik (ML) Yöntemi veya Genelleştirilmiş Momentler Yöntemi (GMM) gibi ekonometrik teknikler kullanılarak tahmin edilir. Daha sonra ise, istatistiksel olarak modelden üretilen veri ile gözlemlenen veri arasındaki farkın sadece örneklem hatasından kaynaklandığı hipotezi test edilir. Kalibrasyon yönteminde ise, modelin gerçek ekonominin doğru bir tanımı olmadığı, sadece onun bir benzeri olduğu varsayılır. Başka bir deyişle modelin “yanlış” olduğu baştan (ex-ante) kabul edilir. Daha sonra, model kalibre edilir ve modelden üretilen veri ile gözlemlenen veri karşılaştırılarak, modelden elde edilen verinin gözlemlenen veriye ne kadar benzediği değerlendirilir. Bu karşılaştırma için genellikle etki-tepki (impulse-response) fonksiyonları ve ikinci momentler kullanılır. Şekil 2'de ekonometrik tahmin ve kalibrasyon yaklaşımlarının DSGD modellerinin geliştirilmesi ve analiz sürecindeki yerleri görülmektedir.

Şekil 2: Kalibrasyon ve Tahmin Yöntemleri ve DSGD Metodolojisi

İktisatçılar arasında DSGD modellerinin değerlendirilmesinde kullanılması gereken yöntem önemli bir tartışma konusu olmuştur (Quah, 1995; King, 1995). Kalibrasyon yaklaşımını savunan iktisatçılar (bkz.Kydland, 1992; Kydland ve Prescott, 1991; Kydland ve Prescott, 1996), geleneksel istatistiksel çıkarım yöntemlerinin eksikliklerini vurgulamış ve bu tekniklerin önemli konularda yeterince bilgilendirici olmadıklarını ileri sürmüşlerdir. Bu yazarlara göre, ekonometrik tahmin DSGD modellerinin veri ile test edilmesi için uygun bir yöntem değildir. Ekonometrik tekniklere dayanarak, bütün modelleri istatistiksel olarak yüksek bir anlamlılık düzeyinde reddetmek mümkündür. Çünkü, modelin “yanlış” olduğu zaten önceden bilinmektedir ve yanlış olduğu bilinen bir modelin yanlışlığının test edilmesi anlamsızdır. Bu iktisatçılara göre, DSGD analizinde izlenmesi gereken yol istatistiksel testler yerine modelin çalışma dinamiklerine yoğunlaşmaktır (King, 1995).

Öte yandan, ekonometrik tahmin yöntemini benimseyen iktisatçıların temel argümanları ise, kalibrasyon yaklaşımında parametre değerlerinin seçiminde sağlam kriterlerin bulunmamasıdır (Canova, 1994). Bu iktisatçılar, yapısal parametrelerin değerlerinin sübjektif kriterlerle belirlenmesi yerine, formel ekonometrik teknikler yardımı ile tahmin edilmesi gerektiğini ileri sürmüşlerdir.

3.1. Tahmin Yöntemi

DSGD literatüründe ekonometrik tekniklerin kullanılması Hansen ve Sargent'ın (1980) yılındaki çalışmaları ile başlamıştır. Bu çalışmadan sonra, DSGD modellerinin tahmin edilmesi amacıyla çeşitli teknikler geliştirilmiştir. Bütün bu tekniklerin temeli, Euler denklemlerinin tahmin edilmesine dayanmaktadır. İki adımlı bir süreçte, önce Euler denklemleri kullanılarak parametreler tahmin edilir ve model simülasyonları elde edilir. Daha sonra ise, elde edilen simülasyonlar ya etki tepki fonksiyonları, veya istatistiksel testler kullanılarak gözlemlenmiş veri ile karşılaştırılır.

Tahmin yönteminin kalibrasyon yöntemine göre bazı avantajları aşağıdaki gibi sıralanabilir (Ruge-Murcia, 2003:2):

1.            Genellikle DGSD modellerindeki varsayımlar, kalibrasyonda kullanılan parametre değerlerinin tahmin edildiği mikro ekonometrik çalışmalardaki varsayımlardan farklı olabilmektedir. Tahmin yöntemlerinde ise, DGSD modelinden elde edilen kısıtlar tahmin sürecinde kullanıldığı için, böyle bir endişe yersizdir.

2.            Kalibrasyon için kullanılacak parametre değerlerinin mikro (disaggregated) veri kullanılarak tahmin edilmesi zor olabilir, veya mümkün olmayabilir. Oysa bu parametreler, rahatlıkla bulunabilen toplulaştırılmış veri kullanılarak tahmin edilebilir.

3.            Tahmin yöntemi kullanıldığında, model sonuçlarının test edilmesi aşamasında güven aralıkları oluşturmak mümkündür. Örneğin, bootstrap tekniği kullanılarak etki-tepki fonksiyonları için güven aralıkları oluşturulabilir. Parametre belirsizliği (parameter uncertainty) düşünüldüğünde, güven aralıklarının oluşturulabilmesi önemli bir avantaj sayılabilir.

4.            DSGD modelinin tahmin edilmesi, ekonometride model seçimi için geliştirilmiş standart yöntemlerin kullanılmasına olanak sağlar. Örneğin tahmin edilen modelin hata kareleri ortalaması bir başka DSGD modeli ile, veya bir VAR tahmini ile karşılaştırılabilir, parametre stabilitesi test edilebilir, veya modelin bazı tanımlanma (identification) varsayımları direkt olarak test edilebilir.

DSGD modellerinde parametre değerlerinin tahmini için regresyon gibi bildik ekonometrik tekniklerin kullanılması mümkün değildir. Bunun en önemli nedeni DSGD modellerinin “tekil” (singular) olmasıdır. Bu modeller, kullanılan dışsal şok sayısından daha fazla politika karar kuralı (içsel değişkenler için dinamik öngörü denklemleri) üretirler.[v] Dolayısı ile, elde edilen denklemler sisteminde bazı değişkenler diğerlerinin doğrusal kombinasyonlarıdır. Diğer bir ifade ile, birçok ekonometrik tahmin yöntemi için gerekli olan “ortogonalite” özelliği mevcut değildir.

Standart ekonometrik teknikler ile ilgili bir başka sorun ise, genellikle bu tekniklerin doğrusal modeller için uygun olmalarıdır. Halbuki, DSGD modelleri için doğrusal olmayan tahmin ediciler gereklidir. DSGD modellerinde yer alan yapısal parametreler, Euler denklemlerine doğrusal olmayan formlarda girerler. Ayrıca bir parametre birden fazla Euler denkleminde yer alır. Bu nedenle, Euler denklemlerini ekonometrik olarak tahmin edebilmek için doğrusal olmayan tahmin edicilere ihtiyaç vardır (Wickens, 1995). DSGD modellerinin tahmininde yaygın olarak kullanılan yöntemlerin bazıları En Çok Olabilirlik (Maximum Likelihood) Yöntemi (Altug, 1989; Leeper ve Sims, 1994), Genelleştirilmiş Momentler Yöntemi (Generalized Methods of Moments) (Hansen ve Singleton, 1982; Eichenbaum ve Hansen, 1990; Kim 2000) ve Simule Edilmiş Momentler Yöntemi (Simulated Methods of Moments) (Duffie ve Singleton, 1993) olarak sıralanabilir.

3.2. Kalibrasyon Yöntemi

Kalibrasyon yaklaşımının, makro ekonomik analizde etkin bir şekilde kullanılmasına öncülük eden iktisatçılar Kydland ve Prescott (1982) ve Prescott (1986) olmuştur. Bu yaklaşım iktisatçılar tarafından benimsenerek DSGD analizlerinde en fazla kullanılan yöntem haline gelmiştir.

Kalibrasyon yöntemi çeşitli araştırmacılar tarafından farklı şekillerde algılanmaktadır. Örneğin bazı yazarlar (bkz. Canova, 1994; Canova ve Ortega, 2000) kalibrasyonu, sadece modeldeki yapısal parametrelere gözlemlenen ekonomik veriyi taklit edebilecek değerler atamak olarak (dar anlam) tanımlarken, Kydland ve Prescott (1996) gibi makro ekonomik literatürde bu yöntemin öncülüğünü yapan yazarlar ise, kalibrasyonu araştırma sorusunun ortaya konması ile başlayan, parametre değerlerinin seçimi, modelin çözümü ve simülasyonların elde edilmesine kadar giden bir süreç (geniş anlam) olarak görmektedir.

Dar anlamdaki kalibrasyon iki adımdan oluşan bir süreç olarak nitelendirilebilir. Birinci adımda, parametre değerleri modelden elde edilen zaman serilerinin gerçek veriyi taklit edebileceği şekilde seçilerek, simülasyonlar elde edilir. İkinci adımda ise, simülasyonlardan elde edilen veriler gerçek verilerle karşılaştırılarak model bir anlamda test edilir. Hansen ve Heckman (1996) bu işlemin istatistiksel anlamda bir “test” olmadığını vurgulamak amacıyla “doğrulama” (verification) terimini kullanmaktadırlar. Bu çalışmada böyle bir “metodolojik” ayrıma gidilmeden her iki terim de eş anlamlı olarak kullanılacaktır.

Kalibrasyon yaklaşımını önererek, tahmin yöntemlerinin DSGD analizine uygun olmadığını savunan yazarlar, klasik istatistiksel testlerin kullanılmasının anlamlı olmadığını ileri sürmüşlerdir. Bu düşünceye göre, bir ekonomik model en iyi ihtimalle, gerçek ‘veri üreten sürecin’ (data generating process) bir benzeri (approximation) olarak görülebilir, ve ne ‘doğru’, ne de ‘gerçekçi’ olmak zorunda olan böyle bir model, istatistiksel olarak test edilebilecek bir sıfır hipotezi olarak değerlendirilmemelidir (Prescott, 1991:5). Daha önce de ifade edildiği gibi, bir ekonomik modelin gerçek veri üreten süreç ile aynı olduğunun kabul edilerek, bunun istatistiksel olarak test edilmesi, başlangıçta yanlış olduğu bilinen bir modelin doğruluğunun test edilmesi anlamına gelir.

Kalibrasyon tekniği DSGD analizi için oldukça kullanışlı bir araç olmasına rağmen, uygulamada bir takım eksiklikleri olduğu üzerinde fikir birliği oluşmuştur. Canova, (1994) kalibrasyon uygulamalarında görülen temel eksiklikleri aşağıdaki gibi sıralamaktadır:

1.            Parametre değerlerinin seçiminde kullanılan kriterler çok farklı ve tartışmalı olabilmektedir.

2.            Model sonuçlarının güven düzeyleri hem teorik modelin güven düzeyine hem de parametre belirsizliğine bağlı olduğundan, teorik modelin başarısını değerlendirmek için enformel tekniklere başvurulmak zorundadır.[vi]

3.            Simülasyon sonuçları seçilen parametre değerlerine bağlıdır ve farklı değerlere karşı oldukça duyarlı olabilmektedir. Bu nedenle Kydland (1992), model sonuçlarının parametre değerlerindeki değişmelere karşı duyarlılık analizlerini kalibrasyon sürecinin bir parçası olarak görmektedir.

 Kalibrasyon tekniği hakkında tartışılan en önemli konu parametre değerlerinin nasıl seçileceğidir. Kydland ve Prescott (1982) simülasyonda kullanılacak parametre değerlerinin seçiminde temel alınacak prensiplerin neler olacağı konusunda çok açık değillerdir. Yazarlar bu ve izleyen çalışmalarında ilgili değişkenlerin zaman serileri ortalamalarını kullanmışlardır. Daha sonraki kalibrasyon uygulamalarında da en sık kullanılan yöntem bu olmuştur (örneğin bkz. Cooley ve Prescott, 1995). Hansen ve Heckman (1996)'a göre ise, kalibrasyonda kullanılacak parametre değerleri güvenilir mikro ekonometrik tahminlerden elde edilmelidir. Ancak, ilgili parametreler üzerine yapılmış olan mikro ekonometrik çalışmaların olmaması veya yetersizliği araştırmacı açısından önemli bir sorun teşkil edebilmektedir. Örneğin bu çalışma boyunca Türkiye ekonomisi için, riskten kaçınma katsayısı ve zamanlararası ikame esnekliği katsayısı gibi temel parametreler üzerine yapılmış bir ekonometrik çalışmaya rastlanılmamıştır.

Doğrulama süreci, yani model simülasyonlarının değerlendirilmesinde enformel yöntemler (Örneğin etki-tepki fonksiyonları veya ikinci momentlerin karşılaştırılması gibi) kullanılması ise  diğer bir tartışma konusunu oluşturmaktadır (Watson, 1993). Kydland ve Prescott (1982) modelin doğrulanması için ilgili değişkenlerin ikinci momentlerini kullanmışlardır. Fakat yazarlar bu süreçte, istatistiksel testler veya belirli bir ölçüt kullanmak yerine sübjektif değerlendirmeler yapmışlardır. Watson (1993) gibi bazı yazarlar, kalibrasyon tekniğine yapılan eleştirilerden yola çıkarak, daha formel doğrulama teknikleri önermişlerdir.[vii]

4.Sonuç

Birçok iktisatçı DSGD modellerini gerçek veri ile karşılaştırmak için kalibrasyon yaklaşımını tercih etmektedirler. Bir başka deyişle,  modelin yapısal parametreleri, modelden elde edilen yapay verinin gerçek ekonomik veriyi taklit edebileceği şekilde enformel tekniklerle seçmektedirler. Kalibrasyon olarak adlandırılan bu yöntem, ekonometrisyenler tarafından enformel, ‘ateorik’ ve etkin olmayan bir yaklaşım olarak kabul edilmekte ve eleştirilmektedir. Ekonometrisyenler bu eleştirilerden hareketle  model öngörülerinin ekonometrik yöntemlerle tahmin edilmesi gerektiğini savunmaktadırlar.

Bu çalışmada DSGD modellerinin ampirik geçerliliğinin sınanmasında izlenilen kalibrasyon ve tahmin yaklaşımları ele alınmıştır. Görüldüğü kadarı ile, her iki yöntemin avantajlarının yanında dezavantajları da mevcuttur. Ekonometrik tahmin yöntemini savunan iktisatçılar kalibrasyon yönteminin enformel ve ateorik olduğunu iddia ederlerken, henüz özellikle büyük ölçekli DSGD modelleri için kullanılabilecek etkin ve problemsiz ekonometrik tahmin yöntemleri geliştirilmediğini göz ardı etmektedirler. Mevcut ekonometrik tahmin yöntemleri bu konuda problemsiz görünmemektedirler.

Netice olarak teorik modelin gerçek veri ile karşılaştırılması için izlenecek yol büyük ölçüde metodolojik bakış açısıyla ilgili, sübjektif bir karardır. Bununla birlikte bu konudaki tartışmalar yakın bir gelecekte sona erecek gibi görünmemektedir.