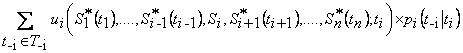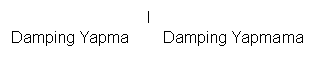önceki

yazdır

 Şevket Alper KOÇ

 Murat HÜCÜMEN

OYUN TEORİSİ MODELLERİ ÇERÇEVESİNDE FİRMALARIN STRATEJİK DAVRANIŞLARININ ANALİZİ

Özet:

Firmalar açısından yapılan modellemelerde teknolojik yapı, piyasa şartları ve yasal prosedürler gibi unsurların firma stratejilerinin belirlenmesinde önemli etkilere sahip olduğu bilinmektedir. Bu makalede firmaların, söz konusu unsurlardan hareketle fiyat, üretim ve diğer politikalarını belirlemekle birlikte, bu politikalarda sürekli olarak kârlarını maksimize edebilecek stratejileri aramaları anlatılmaktadır.

Abstract:

In the firm theory, technological structure, market forces and the legal procedures are very important for the decision of firm strategies in the formation of the models. In this paper, we will analyze how the firms take the price, production and other policies into account and which strategies they will follow in order to maximize their profit.

Giriş

İktisat teorisinin bir dalı olarak mikro iktisat, kendi olanakları çerçevesinde karar veren ve alacağı kararlarla kazancını maksimize etmeye çalışan bireylerin davranışlarını incelemektedir. Bu açıdan bakıldığında birey davranışları bakımından sahip olunan olanaklar ve olanaklar çerçevesinde belirlenen ihtiyaçların giderilmesi şeklinde iki önemli boyut ön plana çıkmaktadır. Söz konusu olanakların temel çerçevesini bireylerin mali yetenekleri belirlemekte ve buradan hareketle malların satın alınması ve hizmetlerin elde edilmesi süreci modellenmektedir. Modellemelerde bütçe kısıtı çerçevesinde faydayı maksimize edebilen mal demetinin belirlenmesi mikro iktisadın temel varsayımı olup, rasyonel davranış açısından önem arz etmektedir.

Firmalar açısından yapılan modellemelerde ise teknolojik yapı, piyasa şartları ve yasal prosedürler gibi unsurların firma stratejilerinin belirlenmesinde önemli etkilere sahip olduğu bilinmektedir. Firmalar, söz konusu unsurlardan hareketle fiyat, üretim ve diğer politikalarını belirlemekle birlikte, bu politikalarda sürekli olarak kârlarını maksimize edebilecek stratejileri aramaktadırlar.[1]

Bireyler açısından faydanın, benzer şekilde firmalar açısından ise kârın maksimizasyonu, mikro iktisat analizlerinin birinci önceliğini oluşturmaktadır. Bu bağlamda mikro iktisat teorisinin ikinci önemli boyutunu denge oluştururken, denge olmaksızın teorik yaklaşımların açıklanması mümkün olamamaktadır. Bu nedenle denge, iktisat teorisinin metodolojik bir unsurudur. Denge yardımıyla ihtimal dahilindeki çeşitli durumlar sınırlandırılabilmekte, bireylerin veya firmaların eş zamanlı davranışları açıklanabilmektedir. İktisat teorisine göre bu sınırlandırmalardan hareketle denge çözümü elde edilmektedir. Yapılan sınırlandırmalar neticesinde hiçbir birey veya firmanın kendi davranışı ile denge durumunu değiştiremeyeceği varsayılmaktadır. Fakat, tek ajanlı karar süreci söz konusu olduğunda, sadece çevre şartlarına optimal derecede uyumlu bir denge süreci dikkate alınmaktadır. Bu bağlamda mikro iktisatta yer alan monopol bir firma, ürünün fiyatını yükseltme veya arzını azaltma yoluyla kârını arttırma çabası içine girebilir.

Çok ajanlı karar durumlarında çevre şartlarının yanı sıra bireyler arasındaki çeşitli etkileşimler de dikkate alınmakta ve interaktif karar sorununda bireylerin kâr veya faydaları diğer bireylerin davranışlarına bağlı olarak şekillenmektedir. Bu tür interaktif durumları dikkate alan analizlerde son yıllarda önemli ilerlemeler kaydedilmiştir. İnteraktif karar sorunu oyun anlamına gelirken, interaktif karar teorisi şeklinde betimlenen teori ise interaktif karar sorununun tahminine ve açıklanmasına olanak sağlayan bununla birlikte oyun teorisi olarak adlandırılan bir yapıyı oluşturmaktadır. Oyun kavramı bağlamında kuşkusuz ajanlar arasındaki etkileşimde sadece bir oyun söz konusu olmayıp, oligopoller arasındaki rekabet durumunda ve firmalar arasındaki öncü firma olma çabalarında olduğu gibi uygulama açısından da farklı süreçler ortaya çıkmaktadır. Oyun teorisinin bireyler ve firmalar açısından dikkate alınan iki önemli unsuru aşağıda sıralanmaktadır.

1) Bütün oyuncular fayda veya kârlarını maksimize etme çabası içindedirler.

2) Strateji kombinasyonları açısından her strateji, diğer oyuncunun stratejisine karşılık verdiği sürece dengenin oluşumuna katkıda bulunur.

Oyun teorisi modellerinde çeşitli stratejiler tercih edilebilmektedir. Stratejiler, genellikle tam bilgi varsayımından ve ihtimal dahilindeki durumlardan hareketle bireylerin hangi stratejileri tercih edebileceklerini ortaya koymaktadır. Genel bir iktisadi yapı dikkate alındığında, bireylerin strateji kombinasyonları zamanla dengeye ulaşmakta, hiçbir bireyin kendi davranışı ile oluşan bu strateji kombinasyonunu değiştirememesi ve tek taraflı olarak kendi faydasını arttıramaması durumunda, farklı birey stratejileri dengesi elde edilmiş olmaktadır. Bu denge, oyun teorisi alanında yapmış olduğu çalışmalardan dolayı John Nash’e atfen “Nash dengesi” olarak adlandırılmaktadır.

1.1- Statik Oyun Modellerinin Ekonomiye Uyarlanması

Statik oyunlar, veri bir zaman dilimi içerisinde oyuncuların, oyundaki diğer oyuncuların hareketlerini bilmeden eş anlı olarak karar vermesi şeklinde oynanan oyunlardır. Oyuncular bir kerelik karar verirler ve oyun sona erer. Statik oyunlar, stratejiler ve kazançlar üzerine odaklanan normal biçimde gösterilmektedir. Bu oyun türü, tam bilgili ve eksik bilgili statik oyunları içine almaktadır. Oyunculardan her birinin, kendisinin ve rakibinin olası strateji kombinasyonları çerçevesinde ortaya çıkan getirilerini bildiği oyunlar olarak tanımlanan tam bilgili statik oyunlar, Nash dengesi vasıtasıyla çözülebilmektedir.

1.2- Nash Dengesi

John Nash’in (1950) yazdığı “Anlaşmasız Oyunlar” makalesi n-kişili sonlu oyunları ve bu oyunların denge noktasını tanımladı. Makalenin giriş bölümünde Nash katkılarını şöyle tanımlar: “Denge noktası fikri bizim teorimizin en önemli parçasıdır. Bu fikir, bizim iki-kişili sıfır-toplamlı oyunların çözümü kavramını genelleştirebilmemizi sağlamaktadır. Sonuç olarak da iki-kişili sıfır-toplamlı oyunların denge noktaları kümesi basitçe karşı iyi stratejilerin kümesi halini alır.” Bir başka ifade ile bir denge noktası bir strateji profilidir ki bu profilde her oyuncunun stratejisi diğer oyuncuların stratejilerine karşı verebildikleri en iyi karşılıktır (best response). Bugün bu denge noktalarına “Nash dengesi” denmektedir.

Nash dengesi kavramının temelinde, en iyi cevap yaklaşımı yer almaktadır. Nash’e göre, iki kişilik bir oyunun çözümüne aday olan strateji çiftini oluşturan oyuncuların stratejilerinin her birinin, rakip oyuncu tarafından oynanacağı tahmin edilen diğer stratejiye en iyi cevap olma niteliğini sağlaması gerekmektedir. Diğer bir deyişle Nash dengesi; rakibinin stratejileri veri iken, her oyuncunun yapabileceğinin en iyisini yaptığına ilişkin bir strateji setidir. İşbirliksiz oyun teorisinin temellerinden birini oluşturan bu dengede, hiçbir oyuncu rakip oyuncunun eylemi sabit alındığında kendi seçimini değiştirmek istemez. Bir başka deyişle hiçbir oyuncu, rakip oyuncunun stratejisi sabit alındığında, kendi eylemini değiştirerek kazancını arttıramaz. Söz konusu Nash dengesinin kendine zorlayıcı ve stratejik istikrar özelliklerini öne çıkardığını söylemek, hiçbir oyuncunun kendi strateji tercihindeki bir sapma aracılığıyla belirtilen dengeden çıkma yönünde bir isteği kalmaması üzerine ifade edilebilecek en uygun karşılıktır. Baskınlık çözümünde ise rakip oyuncunun hangi strateji tercihini gerçekleştirdiğine bakılmadan, oyuncuların, bizzat yapabileceklerinden en iyisini ortaya çıkarma çabasında olduğu bir süreç söz konusu olmaktadır. Sonuç olarak ortaya çıkan dominant strateji dengesi, oyunda tek Nash dengesi olmaktadır.

Statik oyun modelinde, her bir oyuncunun, diğer oyuncunun fiili strateji seçimine en iyi cevabı oluşturacak stratejisini seçtiği varsayılırsa, bu özelliği taşıyan strateji çiftleri oyunun çözümü olacaktır. Bu argüman iki unsur içermektedir.

1) Her oyuncu, rakibinin beklenen strateji seçimine en iyi cevabı oluşturacak olan stratejisini seçmelidir.

2) Denge durumunda, oyuncuların, rakiplerinin strateji seçimleri hakkındaki inançları, bu beklentilerin yerine getirilmiş olması anlamında rasyonel olmalıdır.

Bu gerekliliklerin ilki, bir oyuncunun, rakibinin seçeceği stratejiyi tahmin etmeye çalışacağını varsayarken; ikincisi, aynı oyuncunun, rakibinin oyunu hakkındaki beklentilerinin, rakibi tarafından fiilen oynanan stratejiler ile tutarlı olmasını gerektirir.[2]

İki kişilik bir oyun için Nash dengesinin tanımı sembolik olarak gösterilebilir. Birinci oyuncu, P₁ (s₁^*, s₂^*) ³ P₁ (s₁, s₂^*) koşuluna sahip olmaktadır. P₁, bu oyuncunun Nash dengesi esnasındaki kazancına karşılık gelmekte; s₁ ise birinci oyuncunun stratejilerinden, Nash dengesini meydana getirmeyen seçenek olup, s₁ Î S₁ şeklinde gösterilmektedir. İkinci oyuncu ise, P₂ (s₁^*, s₂^*) ³ P₂ (s₁^*, s₂) şartını elde etmektedir. P₂, bu oyuncunun Nash dengesi esnasındaki kazancına karşılık gelmekte; s₂ ise ikinci oyuncunun stratejilerinden, Nash dengesini meydana getirmeyen seçenek olup, s₂ Î S₂ biçiminde gösterilmektedir. Oyunun Nash dengesi çözümünü, (s₁^*, s₂^*) olarak gösterilen strateji kombinasyonu tanımlamaktadır. Bu tanımın, birinci oyuncuyu içine alan kısmında, s₁^* stratejisinin s₂^* stratejisine en iyi tepki olması; ikinci oyuncuya yönelik olan kısmında ise, s₂^* stratejisinin s₁^* stratejisine en iyi cevap olması yer almaktadır.

Örnek: A ve B harfleri ile gösterilen oyuncular, iki kişilik bir statik oyun oynamaktadırlar. A oyuncusu, A₁ ve A₂; B oyuncusu ise, B₁ ve B₂ stratejilerine sahip olmaktadır. Oyuncuların, karşılıklı olarak seçebilecekleri stratejilere göre elde edecekleri faydalar, aşağıdaki ödül matrisinde belirtilmektedir.

Şekil 1. 2 x 2 lik Oyun Matrisinde Nash Dengesi Çözümü

Yukarıdaki matriste gösterilen tam bilgili statik oyunun çözümünde, Nash dengesi yöntemi kullanılmaktadır. İlk olarak, B oyuncusunun seçimlerine göre A oyuncusunun en iyi tepkileri bulunmaktadır. Eğer sütun oyuncusu B₁ stratejisini tercih ederse, satır oyuncusu 11 > 10 olduğundan A₁ stratejisini seçecektir. Şayet sütun oyuncusu B₂ stratejisini seçerse, satır oyuncusu 6 > 4 olduğundan yine A₁ stratejisini tercih edecektir. Karşılıklı strateji seçimleri sonucunda ortaya çıkan, A oyuncusunun elde edebileceği faydalara denk düşen sayısal değerlerin altına çizgi çekilebilmektedir.

Satır oyuncusunun en iyi tepkileri bulunduktan sonra, bu kez A oyuncusunun tercihlerine göre B oyuncusunun en iyi cevapları bulunmaya çalışılacaktır. Eğer satır oyuncusu A₁ stratejisini tercih ederse, sütun oyuncusu 3 > 1 olduğundan B₂ stratejisini seçecektir. Şayet satır oyuncusu A₂ stratejisini seçerse, sütun oyuncusu 2 > 1 olduğundan B₁ stratejisini tercih edecektir. Karşılıklı strateji seçimleri sonucunda ortaya çıkan, B oyuncusunun sahip olabileceği faydalara denk düşen sayısal değerlerin altına çizgi çekilebilmektedir.

Sonuç olarak, her bir oyuncunun aynı anda yaptığı en iyi seçimden oluşan strateji kombinasyonu Nash dengesini vermektedir. Yukarıdaki kazanç matrisinde yer alan (A₁, B₂) strateji kombinasyonu Nash dengesine karşılık olmaktadır. Oyuncuların bu stratejileri karşılıklı olarak tercih etmeleri neticesinde, satır oyuncusu 6 birim, sütun oyuncusu ise 3 birim fayda kazanmaktadır. Yukarıdaki oyun matrisinde görüldüğü üzere, denge noktasında, her bir oyuncunun faydasına karşılık gelen sayısal değerin altında çizgi bulunmaktadır. Bu analiz bir firma örneği ile güçlendirilebilir. 

Örnek: Mobilya sektöründe faaliyet gösteren iki rakip firma tam bilgili bir statik oyun oynamaktadır. Bu oyun modelinin varsayımları aşağıda belirtilmektedir.

1) Firmalar ürünlerini sabit bir fiyattan satmaktadırlar.

2) Reklam, piyasadaki toplam talep düzeyini etkilememektedir.

3) Mobilya üretip satan firmalar, D ile gösterilen düşük reklam harcaması ve Y ile gösterilen yüksek reklam harcaması stratejilerini seçip uygulayabilirler.

4) Firmaların piyasa payları, seçecekleri reklam harcaması düzeyine bağlıdır.

Oyunun kazanç matrisini oluşturabilmek için bazı ek değişkenlere gerek vardır. P _o, endüstrinin kâr düzeyini; m _{j k} ise rakip firma (k = Y, k = D) anlamına gelen k stratejisini seçtiğinde, diğer firmanın (j = Y, j = D) manasına gelen j stratejisini tercih etmesi durumunda ortaya çıkacak olan piyasa payını göstermektedir. Değişik reklam düzeyi seçimlerinde piyasa payı toplamı bire eşit olmakta ve m _{j k} + m _{k j} = 1 şeklinde yazılmaktadır. Bu oyunda P _o = 2.000.000 YTL, yüksek reklam harcamasını ifade eden R _Y = 800.000 YTL, düşük reklam harcamasını gösteren R _D = 400.000 YTL ve firmaların farklı reklam düzeyi seçimlerine göre elde ettikleri piyasa payları sırasıyla m _YY = 1/2, m _YD = 4/5, m _DY = 1/5, m _DD = 1/2 olmaktadır. Bu veriler yardımıyla A ve B firmasının kazancını hesaplayabilmek için aşağıya kazanç fonksiyonları yazılabilmektedir.

P _A (R _Y, R _Y) = m _YY P _o – R _Y = (1/2) x 2000 – 800 = 200.000 YTL

P _B (R _Y, R _Y) = m _YY P _o – R _Y = (1/2) x 2000 – 800 = 200.000 YTL

P _A (R _Y, R _D) = m _YD P _o – R _Y = (4/5) x 2000 – 800 = 800.000 YTL

P _B (R _D, R _Y) = m _DY P _o – R _D = (1/5) x 2000 – 400 = 0

P _A (R _D, R _Y) = m _DY P _o – R _D = (1/5) x 2000 – 400 = 0

P _B (R _Y, R _D) = m _YD P _o – R _Y = (4/5) x 2000 – 800 = 800.000 YTL

P _A (R _D, R _D) = m _DD P _o – R _D = (1/2) x 2000 – 400 = 600.000 YTL

P _B (R _D, R _D) = m _DD P _o – R _D = (1/2) x 2000 – 400 = 600.000 YTL

Yukarıda gösterildiği gibi her iki firma yüksek reklam harcaması yaparsa, piyasayı yarı yarıya paylaşırlar. Her bir firma 2.000.000 YTL’lik endüstri kârının 1.000.000 YTL’lik kısmını elde ettikten sonra yüksek reklam harcamasına denk gelen 800.000 YTL’yi düşerek 200.000 YTL değerindeki net kâra sahip olabilmektedir.

Şayet A firması yüksek reklam harcaması yaparken B firması düşük reklam harcaması yaparsa, A firması 2.000.000 YTL’lik endüstri kârının 4/5’i olan 1.600.000 YTL’ye sahip olduktan sonra yüksek reklam harcamasına karşılık gelen 800.000 YTL’yi düşerek 800.000 YTL değerindeki net kârı elde edebilirken; B firmasının ise 2.000.000 YTL’lik endüstri kârının 1/5’i olan 400.000 YTL’yi elde ettikten sonra düşük reklam harcamasına denk gelen 400.000 YTL’yi düşmesi sonucunda kazancı sıfıra eşit olmaktadır.

Eğer A firması düşük reklam harcaması yaparken B firması yüksek reklam harcaması yaparsa, A firmasının 2.000.000 YTL’lik endüstri kârının 1/5’i olan 400.000 YTL’ye sahip olduktan sonra düşük reklam harcamasına karşılık gelen 400.000 YTL’yi düşmesi sonucunda net kârı sıfıra eşit olurken; B firması ise 2.000.000 YTL’lik endüstri kârının 4/5’i olan 1.600.000 YTL’yi elde ettikten sonra yüksek reklam harcamasına denk gelen 800.000 YTL’yi düşerek 800.000 YTL değerindeki net kâra sahip olabilmektedir.

Her iki firma düşük reklam harcaması yaparsa da piyasayı yarı yarıya paylaşırlar. Her bir firma 2.000.000 YTL’lik endüstri kârının 1.000.000 YTL’lik kısmına sahip olduktan sonra düşük reklam harcamasına karşılık gelen 400.000 YTL’yi düşerek 600.000 YTL değerindeki net kârı elde edebilmektedir.

Şekil 2. Mobilya Firmaları Matrisinde Nash Dengesi Çözümü

Yukarıdaki ödül matrisinde, şirketlerin, karşılıklı olarak tercih edebilecekleri stratejilere göre sahip olacakları kârlar gösterilmektedir. Matriste yer alan sayısal değerler 1.000 YTL’ye denk gelmektedir. Bahsedilen tam bilgili statik oyunun çözümünde, Nash dengesi yöntemi kullanılmaktadır. İlk olarak, B firmasının seçimlerine göre A firmasının en iyi tepkileri bulunmaktadır. Eğer B şirketi düşük reklam harcaması yapma stratejisini tercih ederse, A şirketi 800 > 600 olduğundan yüksek reklam harcaması yapma stratejisini seçecektir. Şayet sütun oyuncusu yüksek reklam harcaması yapma stratejisini seçerse, satır oyuncusu 200 > 0 olduğundan yine yüksek reklam harcaması yapma stratejisini tercih edecektir. Karşılıklı strateji seçimleri sonucunda ortaya çıkan, A firmasının elde edebileceği kârlara denk düşen sayısal değerlerin altına çizgi çekilebilmektedir.

A firmasının en iyi tepkileri bulunduktan sonra, bu kez satır oyuncusunun tercihlerine göre B firmasının en iyi cevapları bulunmaya çalışılacaktır. Eğer A şirketi düşük reklam harcaması yapma stratejisini tercih ederse, B şirketi 800 > 600 olduğundan yüksek reklam harcaması yapma stratejisini seçecektir. Şayet satır oyuncusu yüksek reklam harcaması yapma stratejisini seçerse, sütun oyuncusu 200 > 0 olduğundan yine yüksek reklam harcaması yapma stratejisini tercih edecektir. Karşılıklı strateji seçimleri sonucunda ortaya çıkan, B firmasının sahip olabileceği kârlara denk düşen sayısal değerlerin altına çizgi çekilebilmektedir.

Sonuç olarak, kazanç matrisinde yer alan {Y, Y} strateji kombinasyonu Nash dengesini vermektedir. Şirketlerin bu stratejileri karşılıklı olarak tercih etmeleri neticesinde, her ikisi de 200.000 YTL kâr elde etmektedir. Denge noktasında, her bir firmanın kârına karşılık gelen sayısal değerin altında çizgi bulunmaktadır. Ancak bu oyunda, her iki oyuncu için, Nash dengesinden daha iyi bir Pareto optimal sonuç vardır. Bahsedilen optimal sonuç, {D, D} strateji kombinasyonuna karşılık gelmektedir. Eğer firmalar bu stratejileri karşılıklı olarak seçme konusunda bağlayıcı bir anlaşma yaparlarsa, her biri 600.000 YTL kâra sahip olabilmektedir.

1.3- Eksik Bilgili Statik Oyunlarda Denge

Statik Bayesyen oyunlar olarak da adlandırılan eksik bilgili statik oyunlar; en az bir oyuncunun, diğer oyuncunun karşılıklı strateji seçimleri sonucunda ortaya çıkan kazancını bilmediği oyunlar şeklinde izah edilmekte ve Bayesyen Nash dengesi aracılığıyla çözülmektedir. N oyunculu bir statik Bayesyen oyunun normal formda gösterimi aşağıdaki bazı kavramları belirtmektedir.[3]

1) İlk olarak oyuncuların hareket alanları, {A₁, A₂, ..........., A_n} biçiminde olmaktadır. Her bir oyuncunun hareket alanı içinde, oyun esnasında oynayabileceği stratejiler yer almaktadır.

2) Oyuncuların tip alanları, {T₁, T₂, .........., T_n} şeklinde yazılmaktadır. Örnek olarak düşük ve yüksek maliyetli strateji harcamaları, tip alanları içerisinde T₁ = {C_H, C_L} ve T₂ = {C_H, C_L} şeklinde betimlenmektedir. Bu alanlar içerisindeki ifadeler sayısal olarak da yazılabilir.

3) Oyuncuların sonuç fonksiyonları, {U₁, U₂, .... U_n} biçiminde yazılmaktadır. Oyuncu i, kendi kişisel tipini bilmekte ve bu sayede kendine özgü sonuç fonksiyonunu saptayabilmektedir. Aynı oyuncunun sonuç fonksiyonu, u_i (a₁, a₂, ...., a_n; t_i) biçiminde tasvir edilmektedir. Fonksiyonda a₁ Î A₁, a₂ Î A₂, ......., a_n Î A_n olmakta ve t_i Î T_i ise i oyuncusunun T_i ile gösterilen olası tip topluluğunun bir üyesi olan t_i’yi ifade etmektedir. Her bir oyuncu, diğer oyuncuların tipleri konusunda kararsız olduğundan bu oyuncuların sonuç fonksiyonları hakkında da emin olamamaktadır.

4) Herhangi bir oyuncu, öteki oyuncuların tipleri ile ilgili inanç sahibidir. Oyuncuların inançları, {P₁, P₂, ..., P_n} şeklinde yazılan koşullu olasılıklardan oluşmaktadır. Oyuncu i’nin, (n – 1) oyuncu hakkındaki inancı p_i(t _–i / t _i) biçiminde belirtilmektedir. Burada, t _–i = (t ₁, t ₂, ...., t _{i – 1}, t _{i + 1}, ...., t _n) ve t ₁ Î T₁, t ₂ Î T₂, ...., t _n Î T_n olmaktadır. Oyuncu i’nin yukarıdaki inancı; aynı oyuncunun kendine özgü tipi t _i göz önünde tutulurken, diğer oyuncuların olası tipleri ile ilgili oyuncu i’nin kararsızlık içinde olduğunu tanımlamaktadır. İki oyuncunun yaptığı düşük ve yüksek maliyetli strateji harcamaları koşullu olasılık biçiminde örnek olarak yazılabilir. Oyuncu 1’in inançları olan olasılıklar; p₁ (C₂ = C_H / C₁ = C_H), p₁ (C₂ = C_H / C₁ = C_L), p₁ (C₂ = C_L / C₁ = C_H), p₁ (C₂ = C_L / C₁ = C_L) ve oyuncu 2’nin olasılıkları; p₂ (C₁ = C_H / C₂ = C_H), p₂(C₁= C_H / C₂ = C_L), p₂ (C₁ = C_L / C₂ = C_H), p₂ (C₁ = C_L / C₂ = C_L) olarak gösterilmektedir. Bu inançlar içindeki harfli ifadeler sayısal olarak da yazılabilir.

5) (S₁^*, S₂^*, ...., S_n^*) şeklinde gösterilen stratejiler, eksik bilgi içeren statik oyunun bir tam strateji Bayesyen Nash dengesidir. Bunun için ön şart; her bir oyuncu i ve t _i Î T_i biçiminde belirtilip stratejileri etkileyen i’nin tiplerinin her biri için aşağıdaki harfli ifade açılımını maksimum yapan S_i Î A_İ değerinin olasılıklar yardımıyla çözülen S_İ^* (t _i) denge strateji değerine eşit olmasıdır.

Eksik bilgili statik oyunların Bayesyen Nash dengesini bulabilmek için Bayes teoremi hakkında bilgi sahibi olmak gerekmektedir.[4]

Örnek: K ve L harfleri ile gösterilen oyuncular, iki kişilik eksik bilgili bir statik oyun oynamaktadırlar. K oyuncusu, A ve B; L oyuncusu ise C ve D stratejilerine sahip olmaktadır. Oyuncuların, karşılıklı olarak tercih edebilecekleri stratejilere göre elde edecekleri faydalar, aşağıdaki ödül matrisinde gösterilmektedir.

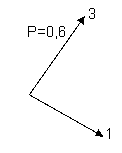
Şekil 3. Tek Değişkenli Statik Bayesyen Oyunun Gösterimi

Oyunun analizi, ilk önce satır oyuncusuna yönelik olarak yapılmaktadır. Eş zamanlı olarak satır oyuncusunun A, sütun oyuncusunun C stratejisini oynaması sonucunda oyuncu K (4 + X) birim fayda; satır oyuncusunun A, sütun oyuncusunun D stratejisini oynaması sonucunda ise aynı oyuncu bu sefer (X) birim fayda elde etmektedir. Ödül matrisindeki X değişkeni satır oyuncusunun tipini belirtmekte ve bu oyuncu doğal olarak kendi tipini bilmektedir. Satır oyuncusu mutlu ise X değişkeni 3, mutsuz ise aynı değişken 1 değerini almaktadır. Eğer X = 3 ise oyuncu L, C stratejisini oynarken satır oyuncusu (4 + 3 = 7) > 6 olduğundan A stratejisini; sütun oyuncusu D stratejisini oynarken oyuncu K (X = 3) > 2 olduğundan yine A stratejisini oynamalıdır. Bu durum, X = 3 iken sütun oyuncusu hangi stratejiyi oynarsa oynasın satır oyuncusunun A stratejisini oynayacağını yani A stratejisinin B stratejisi karşısında dominant bir strateji olduğunu ifade etmektedir. Şayet X = 1 ise oyuncu L, C stratejisini oynarken satır oyuncusu (4 + 1 = 5) < 6 olduğundan B stratejisini; sütun oyuncusu D stratejisini oynarken oyuncu K (X = 1) < 2 olduğundan yine B stratejisini oynamalıdır. Bu durum, X = 1 iken sütun oyuncusu hangi stratejiyi oynarsa oynasın satır oyuncusunun B stratejisini oynayacağını yani B stratejisinin A stratejisi karşısında dominant bir strateji olduğunu göstermektedir.

Oyun, sütun oyuncusuna yönelik olarak da analiz edilebilir. Oyuncu L, satır oyuncusunun tipini kesin bir biçimde bilmemekte yalnızca onu belli olasılıklara göre tahmin etmektedir. Bu bağlamda, sütun oyuncusu X değişkeninin P = 0,6 olasılıkla 3, (1 – P) = 0,4 olasılıkla 1 değerini aldığına inanmaktadır.

Şayet oyuncu K, A stratejisini oynarsa, oyuncu L (4 > 3) olduğundan C stratejisini oynamalıdır. Eğer satır oyuncusu B stratejisini seçerse, sütun oyuncusu (2 > 0) olduğundan bu defa D stratejisini tercih etmelidir. Görüldüğü gibi, satır oyuncusunun strateji seçimleri karşısında oyuncu L farklı stratejileri oynamakta olup bu durum sütun oyuncusunun dominant stratejisinin olmadığını anlatmaktadır. Bu sebepten dolayı oyuncu L’nin inançları önem kazanmaktadır. Eğer sütun oyuncusu C stratejisini oynarken X = 3 olacağına inanırsa, oyuncu K (0,6) olasılıkla A stratejisini oynamalı ve bu sayede oyuncu L (4 x 0,6 = 2,4); aynı oyuncu aynı stratejiyi oynarken X=1 olacağına inanırsa, satır oyuncusu (0,4) olasılıkla B stratejisini oynamalı ve bu sayede oyuncu L (0 x 0,4 = 0) hiçbir faydaya sahip olamamaktadır. Oyuncu L’nin, C stratejisini tercih etmesi neticesinde beklenen kazancı EU(C)=2,4+0=2,4 birim fayda olmaktadır. Şayet sütun oyuncusu D stratejisini oynarken X = 3 olacağına inanırsa, oyuncu K (0,6) olasılıkla A stratejisini tercih etmeli ve bu sayede oyuncu L (3 x 0,6 = 1,8); aynı oyuncu aynı stratejiyi seçerken X = 1 olacağına inanırsa, satır oyuncusu (0,4) olasılıkla B stratejisini tercih etmeli ve bu sayede sütun oyuncusu (2 x 0,4 = 0,8) birim fayda elde etmektedir. Oyuncu L’nin, D stratejisini seçmesi neticesinde beklenen kazancı EU(D) = 1,8 + 0,8 = 2,6 birim fayda olarak bulunmaktadır. EU(D) = 2,6 > EU(C) = 2,4 olduğundan, sütun oyuncusu L için satır oyuncusu K’nın strateji seçimlerine en iyi cevap D stratejisini oynamak olacaktır.

Yukarıdaki eksik bilgili statik oyunun tam strateji Bayesyen Nash dengesi, {(A, X = 3; B, X = 1), D} strateji kombinasyonuna karşılık gelmektedir. Bu ifade, sütun oyuncusu L, D stratejisini oynadığında satır oyuncusu K’nın aynı stratejiye karşı kendi tipi olan X değişkeni 3 ise A, 1 ise B stratejisini seçerek en iyi tepkiyi vereceğini; satır oyuncusu K, sütun oyuncusu L’nin inançlarına göre 0,6 olasılıkla A ve 0,4 olasılıkla B stratejisini tercih ettiğinde sütun oyuncusu L’nin aynı strateji karışımına karşı D stratejisini oynayarak en iyi cevabı vereceğini anlatmaktadır.

Örnek: İki rakip firma olan A ve B, orman ürünleri sektöründe faaliyette bulunmakta, bu çerçevede rabıta üretip satmaktadırlar. Her iki firma da ET ile gösterilen üretim esnasında eski teknoloji kullanımı ve YT ile ifade edilen üretim esnasında yeni teknoloji kullanımı stratejilerine sahiptir. Bu firmalar arasında eksik bilgi içeren bir statik oyun oynanmaktadır. Şirketlerin, karşılıklı olarak seçebilecekleri stratejilere göre kazanacakları kârlar, aşağıdaki sonuç matrisinde belirtilmektedir. 2 x 2 lik oyun matrisinde yer alan sayısal veriler 100.000 YTL’ye denk düşmektedir.

Şekil 4. Rabıta Firmaları Arasındaki Statik Bayesyen Oyun

Oyunun analizi, ilk önce sütun oyuncusuna yönelik olarak yapılmaktadır. Eş zamanlı olarak B firmasının ET, A firmasının da ET stratejisini oynaması sonucunda sütun oyuncusu B (3X) YTL kâra; B şirketinin aynı stratejiyi, A şirketinin ise YT stratejisini seçmesi neticesinde sütun oyuncusu B bu defa (100.000 + 3X) YTL kâra; B firmasının YT, satır oyuncusu A firmasının ise ET stratejisini tercih etmesi sonucunda aynı oyuncu bu kez (300.000 + X) YTL kâra sahip olmaktadır. Ödül matrisindeki X değişkeni sütun oyuncusu B firmasının tipini belirtmekte ve bu oyuncu doğal olarak kendi tipini bilmektedir. Sütun oyuncusu düşük maliyetli teknoloji harcaması yaptıysa X değişkeni 200.000 YTL, yüksek maliyetli teknoloji harcaması yaptıysa aynı değişken 100.000 YTL değerini almaktadır. Eğer X=2 ise satır oyuncusu A, ET stratejisini oynarken sütun oyuncusu B firması da (3 x 2 = 6) > (3 + 2 = 5) olduğundan ET stratejisini; A firması YT stratejisini oynarken B firması [1 + (3 x 2) = 7] > 6 olduğundan yine ET stratejisini oynamalıdır. Bu durum, X = 2 iken satır oyuncusu olan A firması hangi stratejiyi oynarsa oynasın B firmasının ET stratejisini seçeceğini yani ET stratejisinin YT stratejisi karşısında dominant bir strateji olduğunu ifade etmektedir. Şayet X = 1 ise satır oyuncusu olan A firması ET stratejisini oynarken sütun oyuncusu olan B firması (3 x 1 = 3) < (3 + 1 = 4) olduğundan YT stratejisini; A firması YT stratejisini oynarken B firması [1 + (3 x 1) = 4] < 6 olduğundan yine YT stratejisini oynamalıdır. Bu durum, X = 1 iken satır oyuncusu olan A firması hangi stratejiyi oynarsa oynasın B firmasının YT stratejisini tercih edeceğini yani YT stratejisinin ET stratejisi karşısında baskın bir strateji olduğunu göstermektedir.

Oyun, satır oyuncusu olan A şirketine yönelik olarak da analiz edilebilir. A firması, sütun oyuncusu olan B firmasının tipini kesin bir şekilde bilmemekte yalnızca onu belli olasılıklara göre tahmin etmektedir. Bu bağlamda, satır oyuncusu X değişkeninin P = 0,3 olasılıkla 2, (1 – P) = 0,7 olasılıkla 1 değerini aldığına inanmaktadır.

Şayet B firması, ET stratejisini oynarsa, A firması da (4 > 2) olduğundan ET stratejisini oynamalıdır. Eğer sütun oyuncusu YT stratejisini tercih ederse, satır oyuncusu da (5 > 3) olduğundan bu kez YT stratejisini seçmelidir. Görüldüğü gibi, B firmasının strateji tercihleri karşısında A firması farklı stratejileri oynamakta olup bu durum satır oyuncusunun dominant stratejisinin olmadığını izah etmektedir. Bu nedenden dolayı A firmasının inançları önem arz etmektedir. Eğer satır oyuncusu olan A firması ET stratejisini oynarken X=2 olacağına inanırsa, sütun oyuncusu olan B firması da (0,3) olasılıkla ET stratejisini oynamalı ve bu sayede A firması (400.000 x 0,3 = 120.000); aynı oyuncu aynı stratejiyi oynarken X = 1 olacağına inanırsa, B firması (0,7) olasılıkla bu defa YT stratejisini seçmeli ve bu sayede A firması (300.000x0,7 = 210.000) YTL kâr elde etmektedir. A firmasının ET stratejisini tercih etmesi sonucunda beklenen kazancı, EU(ET) = 120.000 + 210.000 = 330.000 YTL olmaktadır. Şayet A firması YT stratejisini oynarken X = 2 olacağına inanırsa, B firması (0,3) olasılıkla ET stratejisini tercih etmeli ve bu sayede A firması (200.000 x 0,3 = 60.000); aynı oyuncu aynı stratejiyi oynarken X = 1 olacağına inanırsa, B firması da (0,7) olasılıkla YT stratejisini oynamalı ve bu sayede A firması (500.000 x 0,7 = 350.000) YTL kâr sağlamaktadır. A firmasının YT stratejisini seçmesi sonucunda beklenen kazancı, EU(YT)=60.000 + 350.000 = 410.000 YTL olarak bulunmaktadır. EU(YT)=410.000 > EU(ET) = 330.000 olduğundan, A firması için B firmasının strateji tercihlerine en iyi tepki YT stratejisini oynamak olacaktır.

Yukarıdaki statik Bayesyen oyunun tam strateji Bayesyen Nash dengesi, {YT, (ET, X = 2; YT, X = 1)} strateji kombinasyonuna denk düşmektedir. Bu ifade, A firması YT stratejisini oynadığında B firmasının aynı stratejiye karşı kendi tipi olan X değişkeni 2 ise ET, 1 ise YT stratejisini seçerek en iyi cevabı vereceğini; B firması, A firmasının inançlarına göre 0,3 olasılıkla ET ve 0,7 olasılıkla YT stratejisini seçtiğinde, A firmasının aynı strateji karışımına karşı YT stratejisini oynayarak en iyi tepkiyi vereceğini göstermektedir.

2.1- Dinamik Oyun Modellerinin Ekonomiye Uygulanması

Dinamik oyunlar, karar almanın bir dizimselliğe sahip olduğu türden oyunlardır. Bu anlamda, çok sayıda zaman diliminde kararlar alınmakta ve oyuncular belirli bir sıralamaya göre hareket etmektedir. Dinamik oyunlar arasında en meşhur örnek satrançtır. Bu oyun türü, kusursuz ve kusurlu bilgili dinamik oyunlar şeklinde ikiye ayrılabilmektedir. Sonraki oyuncunun, kendisinden önce hareket edenlerin davranışlarını bilerek hareket ettiği oyunlar biçiminde tanımlanan kusursuz bilgili dinamik oyunlar, iktisadi ilişkilerin tarihsel bir süreçte geliştiği durumlara uygundur. Bir piyasada yerleşik olan firmaların, kararlarını, piyasaya yeni şirketlerin girip girmeyeceği hesapları üzerine kurması buna bir örnektir. Ayrıca piyasadaki yerleşik firmalar arasındaki pazarlık süreci de dinamik oyunlar ile incelenmeye uygundur. Kusursuz bilgili dinamik oyunların çözüm kavramına bakıldığında, alt oyun mükemmel Nash dengesi üzerine kurulduğu görülmektedir.

2.2- Alt Oyun Kusursuz Nash Dengesi

1965 yılında Reinhard Selten, Nash dengesini, oyuncuların sıra ile stratejilerini tercih ettikleri dinamik oyunlarda kullanılabilecek şekilde geliştirmiştir. Alt oyun kusursuz Nash dengesi ifadesinde yer alan alt oyun kavramının özellikleri aşağıda belirtilmektedir.[5]

1) Oyun ağacında bulunan bir alt oyun, bir karar noktasını kapsayan bir bilgi setinde başlamaktadır.

2) Kusursuz bilginin olduğu bir oyunda, ikincil bir oyun, başlangıç ve bitim noktaları hariç orjinal oyunun karar noktalarının ve hareketlerinin bazılarından oluşur. Alt oyun, orjinal oyunun içerisinde, ondan daha küçük bir oyun olarak düşünülebilir. Kimi zaman bir alt oyun, orijinal oyundaki oyuncuların tamamını içermeyebilir. İki hareket ve bir karar noktasından oluşan, yalnızca bir oyuncunun olduğu alt oyunlar da mevcuttur. Alt oyun bir oyun olduğu için bir başlangıç karar noktası içermekte ve bu nokta asıl oyunun ikincil kökü durumundadır. Özetle bir alt oyun, ikincil kök ve ondan sonra gelen ardılların hepsinden oluşmaktadır. Ayrıca alt oyundaki oyuncuların bitim noktasındaki ödülleri, orijinal oyundaki ödülleri ile aynıdır.

3) Bir alt oyun, asıl oyunun hiçbir bilgi setini kesmemektedir. Yani, bilgi setinin bir düğüm noktası bir alt oyuna ait olurken bu bilgi setinin tüm karar noktaları da aynı ikincil oyuna ait olmak zorundadır.

Şekil 5. İki Oyunculu Bir Oyun Ağacının Gösterimi

Yukarıdaki, iki oyunculu yayvan biçimde gösterilen kusursuz bilgili dinamik oyunda başlangıç noktası oyuncu 1’in altında yer alan noktadır. Oyunun bitim noktaları ise iki oyuncunun elde edeceği faydaların üstünde olan noktalardır. Bu noktalarda, soldaki sayısal değer oyuncu 1’in, sağdaki sayısal veri ise oyuncu 2’nin faydası olmaktadır. A – D yolu, başlangıç karar noktası ile terminal noktası arasındaki iki kenara, A yolu ise oyunun kökü ile oyuncu 2’nin karar noktası arasındaki dala karşılık gelmektedir. Oyunun analizini yapabilmek için önce oyuncuların stratejileri ve bu stratejileri oynadıkları zaman elde edecekleri faydalar tayin edilmelidir. Stratejilerin belirlenebilmesi için oyuncuların yapabilecekleri hareketlerin listesi oluşturulmalıdır. Çünkü dinamik oyunda strateji bir hareket değil, oyun anında oluşabilecek tüm olası durumlar karşısında bir oyuncunun hareketlerinin bütünsel bir tanımıdır. Bu oyunda oyuncu 1 için bir karar noktası vardır. Bu nedenle aynı oyuncu için bir strateji; A, B, C hareketlerinden birini seçmekten ibarettir. Oysa oyuncu 2 için bir strateji, üç karar noktası olması sonucu, oyuncu 1’in önceden yapacağı davranışa bağlı olarak D veya E kararından oluşmaktadır. Oyuncu 2 için olası stratejilerden biri; oyuncu 1 A kararını benimserse D, B kararını benimserse D ve C kararını benimserse E davranışını gerçekleştirmek olacaktır. Bu biçimde oyuncu 2’nin sekiz stratejisi mevcut olmaktadır. Aşağıda iki oyunculu dinamik oyunun stratejik formu verilmektedir.

Şekil 6. İki Oyunculu Dinamik Oyunun Stratejik Formu 

Yukarıdaki matriste, oyuncuların olası her strateji profili sayesinde sahip olacakları faydalar gösterilmektedir. Bu stratejik form daha önce anlatılmış olan Nash dengesi metoduyla çözülmektedir. Bilindiği gibi Nash dengesi, diğer oyuncuların veri denge strateji kullanımına göre her oyuncunun stratejisinin optimal olduğu bir strateji profilidir. Herhangi bir oyuncu tarafından yapılan strateji değişikliği optimal altı ödüle neden olmaktadır. Oyuncu 2, DDE stratejisini tercih ederse oyuncu 1, C stratejisini oynamak zorunda kalacaktır. Şayet oyuncu 1, C stratejisini seçerse oyuncu 2 DDE stratejisini oynayarak diğer herhangi bir strateji tercihine göre daha iyi olur. Bu nedenle strateji profili (DDE, C) bir Nash dengesidir. İkinci olarak, oyuncu 1, A stratejisini oynarsa oyuncu 2, EDD stratejisini tercih ederek diğer strateji seçimlerine göre daha iyi olmaktadır. Eğer oyuncu 2, EDD stratejisini seçerse, oyuncu 1 A stratejisini oynamalıdır. Bu sebeple (EDD, A) strateji profili bir Nash dengesidir. Son olarak, oyuncu 2, EDE stratejisini oynarsa oyuncu 1, C stratejisini seçmelidir. Şayet oyuncu 1, C stratejisini tercih ederse oyuncu 2, EDE stratejisini seçerek diğer strateji tercihlerine göre daha iyi olmaktadır. Strateji profili (EDE, C) bir Nash dengesidir. Üç sonuçtan hangisinin daha muhtemel olduğunun tespit edilebilmesi için Zermelo’nun geliştirdiği geriye doğru tümevarım yöntemi kullanılmaktadır. Böylece çoklu Nash dengesinden biri seçilebilir. Geriye doğru tümevarım yöntemi beş aşamadan meydana gelmektedir.[6]

1) Oyunun bitim noktasından başlanır ve bitim noktasından önceki karar noktasına doğru gidilir. Bu karar noktası oyunculardan herhangi birine aittir. Oyunculardan bazılarına ait olan, terminal noktasından önceki bu karar noktaları; esas, önemsiz ya da karma-bileşik olarak adlandırılmaktadır. Bir düğüm noktasının dallarının her biri tam olarak bir bitim noktasına uzanıyorsa bu esas karar noktasıdır. Yalnızca bir tane kenarı olan esas bir düğüm noktası önemsiz karar noktasıdır. Bir karar noktası esas karar noktası değil ise karma-bileşiktir. Bir önemsiz karar noktasına ulaşıldıktan sonra, karma-bileşik veya bir esas karar noktasına ya da gidilebildiği kadar yukarıya hareket edilir.

2) Birinci adımda ulaşılan her bir esas karar noktasında optimal hareket; bu karar noktasından varılan herbir bitim noktasında, karar noktasının sahibi olan oyuncunun elde edeceği ödüllerin birbiriyle karşılaştırılmasıyla bulunur. Karar noktasında birden daha fazla optimal olan karar söz konusu ise tahsis edilen ödüllerin yeniden değerlendirilmesi ve bu zinciri kıracak bir yol bulmak gerekir. Modeli kuran, zincirin, oyunun doğru bir formülasyonundan oluştuğuna inanıyorsa bir seçimi diğerine göre daha çok muhtemel hale getiren bir sosyal geleneğin olup olmadığını tespit etmeye gerek vardır. Böyle bir gelenek varsa bu zincir bozularak kırılmış olur. Başvurulacak bir uzlaşma ya da gelenek yoksa oyuncuların bu karar noktasındaki davranışlarının tahmin edilemez olduğu kabul edilir.

3) İkinci aşamada yapılan tetkik sonunda, esas karar noktalarından çıkmış optimal olmayan dallar silinir. Bu esas karar noktalarının herbiri, önemsiz karar noktasına dönüşür.

4) Bu safhaya gelindiğinde orijinal oyun daha basit bir oyun haline dönüşmüş olur. Üçüncü adımda oyun ağacının köküne ulaşılmışsa işlemler tamamlanmış olur. Fakat henüz oyun ağacının köküne ulaşılmamışsa yukarıdaki işlemler gelinen karar noktasında tekrar edilir. Bu işlemler oyun ağacının köküne ulaşılıncaya kadar sürdürülür.

5) Her oyuncu için aynı oyuncunun düğüm noktalarının herbirinde optimal kararlar bir arada toplanır. Kararların bu koleksiyonu, o oyuncunun oyundaki optimal stratejisini oluşturur.

Şekil 7. İki Oyunculu Oyunun Budanmış Oyun Ağacı

İki oyunculu dinamik oyunda yukarıdaki şekilde görüldüğü üzere geriye doğru tümevarım yöntemi uygulanmaya başlanmıştır. Bu oyunda, oyuncu 2’nin karar noktalarından başlayan 3 tane alt oyun bulunmaktadır.  Oyuncu 1’in oynayabileceği stratejilere göre oyuncu 2, budanmamış oyun ağacının solundaki alt oyunda (4 < 6) olduğundan E stratejisini; ortasındaki alt oyunda (8 > 7) olduğundan D stratejisini; sağındaki alt oyunda ise (0<5) olduğundan E stratejisini tercih edecektir. Buna bağlı olarak, oyuncu 2’nin üç karar noktasındaki optimal olmayan hareketleri oyun ağacından budanarak, oyuncu 1’e ait önemsiz olmayan bir esas karar noktası bırakılmıştır. Oyuncu 1, kendisinden sonra rasyonel olan oyuncu 2’nin optimal bir strateji oynayacağını varsaymaktadır. Buna dayanarak, oyuncu 1, A stratejisini seçerse oyuncu 2, E stratejisini oynayacak ve oyuncu 1, 3 birim fayda elde edecektir. Oyuncu 1, B stratejisini tercih ederse oyuncu 2, D stratejisini oynayacak ve oyuncu 1, 2 birim faydaya sahip olacaktır. Oyuncu 1, C stratejisini oynarsa oyuncu 2, E stratejisini seçecek ve bunun sonucunda oyuncu 1, 6 birim fayda kazanacaktır. 2 < 3 < 6 olduğundan oyuncu 1 için optimal strateji C hareketidir. Böylelikle dinamik oyunun alt oyun kusursuz Nash dengesi {C, E} strateji profili olmaktadır. Oyuncu 1, 6 birim fayda elde ederken oyuncu 2, 5 birim faydaya sahip olmaktadır.

Örnek: Giriş caydırmacası oyunu, dinamik oyunların kapsamında yer almaktadır. Turistik bir beldede monopol vaziyette faaliyet gösteren I oteli 850.000 YTL kâr elde etmektedir. E oteli de aynı kesimde hizmet ifa edip etmemeye karar vermeye çalışmaktadır. Eğer bu otel yörede faaliyette bulunmaya kalkışmazsa hiçbir şey kazanamamaktadır. Şayet E oteli bu piyasaya girmeye karar verirse, bunu fark eden I oteli konaklama fiyatında damping yapıp yapmama kararı vermek zorundadır. I oteli fiyatta indirime gitmemeye karar verirse, kendisi piyasayı E oteliyle yarı yarıya paylaşmak suretiyle (850.000 / 2 = 425.000) YTL sahibi olurken E oteli giriş maliyetinin 300.000 YTL olmasından dolayı (425.000 – 300.000 = 125.000) YTL elde etmektedir. I oteli fiyatta iskonto yapmaya karar verirse, tatil lüks mal olarak düşünüldüğünden ve talep esnekliği yüksek olduğundan kendisi 570.000 YTL kazanırken I oteli (850.000 – 570.000 – 300.000 = -20.000) YTL zarar etmektedir. Aşağıda gösterilen kusursuz bilgili dinamik oyun ağacında, terminal noktalarının solundaki değerler E oteline, sağındaki veriler ise I oteline ait olmaktadır.

Şekil 8. Oteller Arasındaki Oyunun Oyun Ağacı

Yukarıdaki dinamik oyunun analizini yapabilmek için öncelikli olarak stratejiler belirlenmelidir. E otelinin bir karar noktası mevcuttur. Bu sebeple E oteli için bir strateji, piyasaya girip girmeme hareketinden birini tercih etmekten ibarettir. I otelinin de bir karar noktası vardır. I oteli için ise bir strateji, E otelinin piyasaya girme kararına bağlı olarak fiyat dampingi yapıp yapmama hareketinden birini seçmekten ibarettir. Stratejilerin belirtildiği oyunun stratejik formu aşağıda gösterilmektedir.

Şekil 9. Oteller Arasındaki Oyunun Stratejik Formu

I oteli damping yapma stratejisini oynarsa, E oteli piyasaya girmeme stratejisini tercih etmek zorunda kalacaktır. Diğer yönden E oteli piyasaya girmeme stratejisini seçerse, I oteli fiyat dampingi yapma stratejisini oynamak suretiyle diğer stratejisini tercih etmek kadar sonuç elde etmektedir. Bu nedenle {Girmeme, Damping Yapma} strateji kombinasyonu bir Nash dengesidir. Geriye doğru tümevarım metoduyla da aynı Nash dengesine ulaşmak mümkündür.

Şekil 10. Oteller Arasındaki Oyunun Budanmış Oyun Ağacı

Oteller arasında oynanan dinamik oyunda yukarıdaki şekilde görüldüğü üzere geriye doğru tümevarım yöntemi uygulanmaya başlanmıştır. Bu oyunda, I otelinin karar noktasından başlayan bir tane alt oyun bulunmaktadır. E otelinin oynayabileceği stratejiye göre I oteli, budanmamış oyun ağacındaki alt oyunda 570 > 425 olduğundan fiyat dampingi yapma stratejisini seçecektir. Buna bağlı olarak, I otelinin karar noktasındaki optimal olmayan hareketi oyun ağacından budanarak, E oteline ait önemsiz olmayan bir esas karar noktası bırakılmıştır. E oteli, kendisinden sonra rasyonel olan I otelinin optimal bir strateji oynayacağını varsaymaktadır. Buna dayanarak, E oteli piyasaya girme stratejisini seçerse, I oteli fiyat dampingi yapma stratejisini tercih edecek ve E oteli 20.000 YTL zarar sahibi olacaktır. E oteli piyasaya girmeme stratejisini oynarsa hiçbir şey elde edememektedir. –20.000 < 0 olduğundan E oteli için optimal strateji piyasaya girmeme hareketidir. Bu oyunun alt oyun mükemmel Nash dengesi, {Piyasaya girmeme} stratejisi olarak bulunmaktadır. E oteli hiçbir şey kazanamazken, I oteli 850.000 YTL elde etmektedir.

2.3- Eksik Bilgili Dinamik Oyunlarda Denge

Bir oyuncunun, sahip olduğu stratejilerden birini tercih ettikten sonra diğer oyuncunun bu kararı bilmeksizin elindeki stratejilerden birini seçmesi durumunda ortaya çıkan yapı, tam bilgiye sahip olmayan dinamik oyun olarak isimlendirilmektedir. Bu tür oyunlar için yapılabilecek diğer bir tanım ise eş zamanlı hareket eden oyunculardan oluşan statik oyunların yayvan biçimdeki gösterimi şeklinde olmaktadır. Kusurlu bilgili dinamik oyunlarda bilgi seti kavramı önemli bir yer işgal etmektedir. Bilgi setinin özellikleri aşağıda sıralanmaktadır.[7]

1) Bir oyuncu için bir bilgi seti karar noktalarının toplamından meydana gelmektedir. Eksik bilgili dinamik oyunlarda bulunan ve kesik çizgi ile gösterilen bilgi seti ise en az iki karar noktasını içermekte ve oyuncu bu düğüm noktalarında hareket halinde bulunmaktadır. Ayrıca oyunun hareketi bilgi setindeki bir düğüm noktasına uzandığı sırada kesik çizgi üzerinde yer alan hareketli oyuncu bilgi setinde hangi karar noktasına erişilip erişilmediğini bilmemektedir.

2) Bir bilgi setindeki tüm karar noktaları aynı oyuncuya ait olmalıdır.

3) Bilgi setindeki her bir düğüm noktasında, oyuncu, uygulanabilir aksiyonların aynı setine sahip olmalıdır.

Örnek: Oyuncu 1 ile oyuncu 2 arasında tam bilgili, oyuncu 2 ile oyuncu 3 arasında ise eksik bilgili dinamik oyun oynanmaktadır. Oyuncu 1 A ve B, oyuncu 2 C ve D, oyuncu 3 ise E ve F stratejilerine sahip olmaktadır. Aşağıda gösterilecek olan yayılan biçimdeki oyunda, bitim noktalarının başındaki sayısal değerler oyuncu 1’e, ortasındaki veriler oyuncu 2’ye, sonundaki fayda rakamları ise oyuncu 3’e ait olmaktadır.

Aşağıdaki tam bilgiye sahip olmayan dinamik oyun ağacındaki oyuncuların denge stratejilerinin ve sonuçlarının çözümü için geriye doğru tümevarım yöntemi kullanılmaktadır. İlk olarak, oyuncu 1’in seçebileceği stratejiye göre sol alt oyun analiz edilmektedir. Buna göre oyuncu 2; C stratejisini de oynasa 7 > 6 olduğundan oyuncu 3 E stratejisini, D stratejisini de oynasa 5 > 4 olduğundan oyuncu 3 aynı stratejiyi tercih edecektir. Bu sebeple oyun ağacında oyuncu 3’ün E stratejileri kalın çizgilerle belirtilmekte, F stratejileri ise önemsenmemektedir. Geriye doğru tümevarım metodunun bir sonraki aşamasında ise aynı alt oyunda oyuncu 3’ün E hareketini seçeceğini bilen oyuncu 2 9 > 7 olduğundan C stratejisini oynamalıdır. Bu yüzden oyuncu 2’nin C stratejisi kalın çizgiyle gösterilmekte, D stratejisi ise oyun ağacından budanmaktadır.

Şekil 11. Üç Oyunculu Eksik Bilgili Oyunun Ağacı

İkinci olarak, oyuncu 1’in tercih edebileceği stratejiye göre sağ alt oyun analiz edilmektedir. Buna göre oyuncu 2; C stratejisini de oynasa 2 > 1 olduğundan oyuncu 3 F stratejisini, D stratejisini de oynasa 9 > 8 olduğundan oyuncu 3 aynı stratejiyi seçecektir. Bu nedenle oyun ağacının sağ alt oyununda F stratejileri kalın çizgilerle belirtilmekte, E stratejileri ise oyun ağacından silinmektedir. Geriye doğru tümevarım yönteminin bir sonraki safhasında ise aynı alt oyunda oyuncu 3’ün F davranışını tercih edeceğini bilen oyuncu 2 6 > 4 olduğundan D stratejisini oynamalıdır. Bu yüzden oyuncu 2’nin D stratejisi kalın çizgiyle gösterilmekte, C stratejisi ise oyun ağacından budanmaktadır.

Şekil 12. Eksik Bilgili Oyunun Budanmış Oyun Ağacı

Son olarak, oyuncu 1, kendi tercih edebileceği stratejilere göre oyuncu 2’nin ve oyuncu 3’ün hangi stratejileri oynayabileceğini tahmin etmektedir. Eğer oyuncu 1 A stratejisini seçerse, oyuncu 2 C, oyuncu 3 ise E stratejisini tercih edecek ve sonuçta oyuncu 1 5 birim fayda elde edecektir. Şayet oyuncu 1 B stratejisini oynarsa, oyuncu 2 D, oyuncu 3 ise F stratejisini seçecek ve neticede oyuncu 1 3 birim faydaya sahip olacaktır. 5 > 3 olduğundan oyuncu 1 için yukarıdaki şekilde kalın çizgiyle gösterilen A stratejisini tercih etmek optimal bir davranıştır. Oyuncular bazında bu dinamik oyunun dengesi, {A, C, E} strateji kombinasyonu olmaktadır. Bu sayede oyuncu 1 5 birim, oyuncu 2 9 birim ve oyuncu 3 7 birim fayda kazanmaktadır.

Sonuç

Oyun teorisi, ekonomik faaliyetlere ilişkin en iyi kararın verilmesi için geliştirilmiş matematiksel bir yaklaşımdır. Bu faaliyetlerde birden fazla karar verici, kendi kazançlarını en iyi duruma getirecek biçimde karar vermek zorundadırlar. Oyun teorisi, gruptaki oyuncuların yapabileceklerinin stratejik bir analizine dayanarak, rasyonel seçimler yapan bir grup oyuncu arasındaki var olan karşılıklı etkileşimi analiz eder.[8] Teorinin temelleri yaklaşık 150 yıl geriye, konunun esas gelişimi son 50 yıla dayanmaktadır. Oyun teorisi ekonomik alanda ilk olarak, aksak rekabet piyasalarının analizinde kullanılmıştır. Fransız ekonomist Augustin Cournot’un 1838 yılında yayınladığı “Servet Teorisinin Matematiksel Prensipleri Üzerine Araştırmalar” adlı kitabı üretici rekabeti konusundadır. Kitabının 7. bölümünde düopolün özel bir durumunu, Nash dengenin sınırlandırılmış bir uyarlaması niteliğinde bir çözüm düşüncesinden yararlanarak tartışmıştır.

Modern oyun teorisinin kurucusu olarak tanınan ve satranç, poker, briç gibi oyunlarda oyuncuların davranışlarını modellemek ve akılcı strateji seçimleri üzerine çalışmış olan Macar asıllı Amerikalı John von Neuman, 1928 yılında bütün iki kişilik sıfır toplamlı oyunlarda her oyuncu için birçok stratejinin belirlenmekte olduğunu “Stratejik Oyunlar Teorisi Üzerine” adlı makalesinde ortaya koymuştur. Aynı zamanda hidrojen bombası ve ilk bilgisayarın mucitlerinden sayılan, istatistik, soyut topoloji ve doğrusal programlama konularının içerdiği çok sayıda alana önemli katkılar yapmış çok yönlü bir bilim adamı olan John von Neuman ve ekonomist Oscar Morgenstern birlikte “İktisadi Davranış ve Oyunlar Teorisi” adlı kitabı 1944 yılında yayınladılar ve oyun teorisini ilk defa ekonomi alanına taşıdılar. Neuman ve Morgenstern bu kitapla oyunun kavramsal olarak şekillenmesinde üç önemli katkıda bulundular. Birincisi, oyuncuların oyunu oynamaktan ötürü elde edeceklerini açıklayan, fayda teorisi temeline dayanan bir aksiyom; ikincisi, iki kişilik sıfır toplamlı oyunlar için optimal çözümlerin tanımlanması; üçüncüsü, işbirlikçi oyunların bir versiyonunun gösterilmesidir.[9]

Bu muhteşem çalışmalardan sonra birçok iktisatçı oyun teorisi modellerine hem katkıda bulunmuşlardır hem de bu modelleri ekonominin çeşitli birimlerine uygulamışlardır. Bu makalede ise oyun teorisi modelleri çerçevesinde firmaların stratejik davranışları incelenmiştir ve firmaların stratejik davranışlarını oyun teorisi modelleri ile de analiz edilebileceği gösterilmiştir. Statik ve dinamik oyunlara firma örnekleri verilerek bu oyunların nasıl çözüleceği gösterilmiştir. Önce tam bilgi altında modeller çözümlenmiş, daha sonra eksik bilgi olduğu durumda modellerin nasıl çözüleceği gösterilmiştir. Kavramlar verilen örneklerle desteklenmiştir.